Trzy najciekawsze krzywe w hydraulice

Krótko o płynach

Płyn to każda substancja charakteryzująca się łatwością zmieniania wzajemnego położenia cząstek nawet dla niewielkich sił. W wyniku płyn może swobodnie przemieszczać się (przepływać) przyjmując kształt naczynia, w którym się znajduje. Podstawową cechą płynów jest ich lepkość. Charakterystyczna dla płynów jest łatwość przechodzenia ze stanów statycznych do dynamicznych.

Mechanika płynów jest to dział mechaniki ośrodków ciągłych, zajmujący się analizą ruchu płynów obejmujących zarówno ciecze jak i gazy. Celem tej nauki jest badanie własności płynu (gęstość, temperatura) i własności danego przepływu (prędkości, ciśnienie) w przestrzeni i czasie.

Hydraulika jest to nauka o praktycznych zastosowaniach cieczy, a w szczególności wykorzystywaniu ich ruchu (przepływu). Jest powiązana z mechaniką płynów, która stanowi jej teoretyczną podbudowę.

Płynem, który towarzyszy człowiekowi od zarania dziejów jest niezbędna do życia woda. Dzięki swym szczególnym właściwościom mechanicznym jest również wykorzystywana do transportu, kształtowania  i podporządkowania otoczenia. Aby ujarzmić wodę i wykorzystać jej cenne właściwości ludzie zaczęli budować przemyślne urządzenia z dostępnych materiałów adekwatnych do etapu rozwoju myśli technicznej. Pierwsze znane urządzenia wodne powstały na terenie starożytnego Babilonu i były wykonanymi z drewna kołowymi podnośnikami wody służącymi do nawadniania upraw rolnych. Konstrukcja urządzeń i maszyn wodnych związana jest z rozwojem matematyki, a w szczególności z pracami:

• Archimedesa z Syrakuz (287–212 p.n.e.),
• Leonarda Fibonacciego z Pizy (1175 r. – 1250 r.),
• Daniela Bernoulliego (1700 r.-1782 r.).

Wymienieni myśliciele stworzyli zapisy matematyczne odtwarzające niektóre istotne zasady geometryczne obowiązujące w świecie przyrody zarówno nieożywionej jak i ożywionej.

Spirala Archimedesa

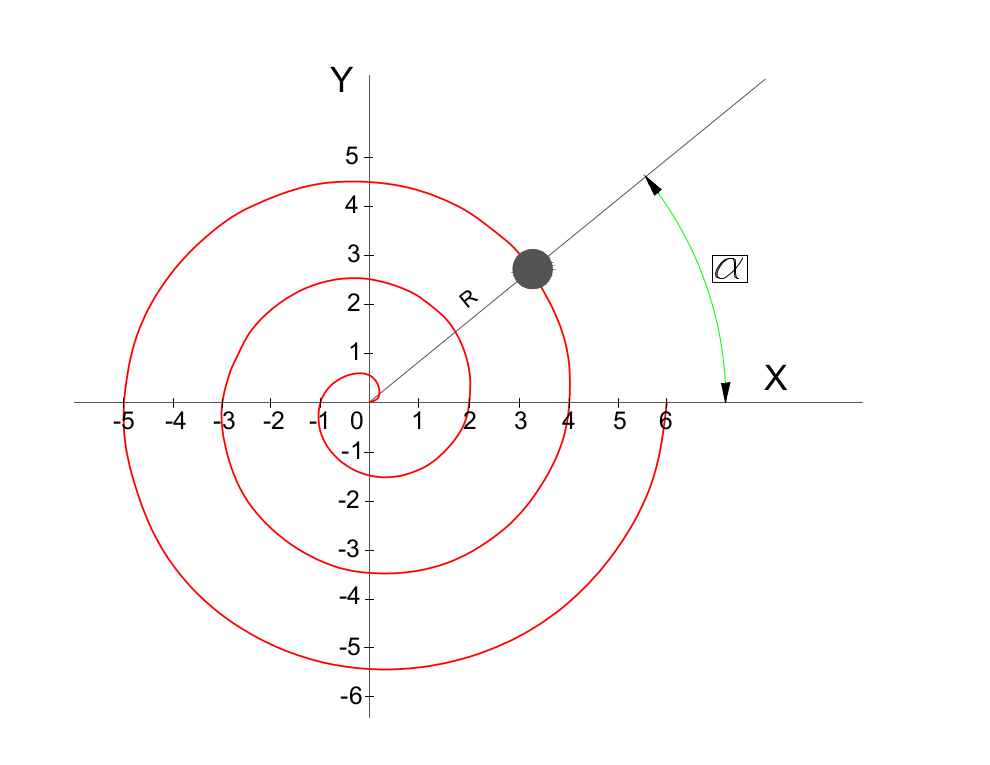
Spiralę taką zakreśla punkt, który porusza się jednostajnie po półprostej, która również jednostajnie obraca się wokół swojego początku. Cechą tej spirali jest jednakowa odległość między zwojami, ponieważ istnieje liniowa relacja pomiędzy kątem a promieniem. W przyrodzie krzywą Archimedesa najlepiej odwzorowuje  sieć pajęcza.

Spirala Fibonacciego

Spirala Fibonacciego opiera się na ciągu liczb, który ma taką właściwość, że wynik dzielenia kolejnej liczby ciągu przez poprzednią liczbę dąży do wartości f= 1,6180339… czyli tzw. boskiej lub złotej proporcji.

W ciągu (szeregu) Fibonacciego każda kolejna liczba jest sumą dwóch poprzednich liczb, stąd jego zapis matematyczny przedstawia się następująco:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, etc…

Na przykład:
0 +1 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
i dalej 144 + 89 = 233

Spiralę Fibonacciego rysuje się w prostokącie zbudowanym z kolejnych  kwadratów o długości boków odpowiadającej kolejnym liczbom ciągu, czyli: 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.

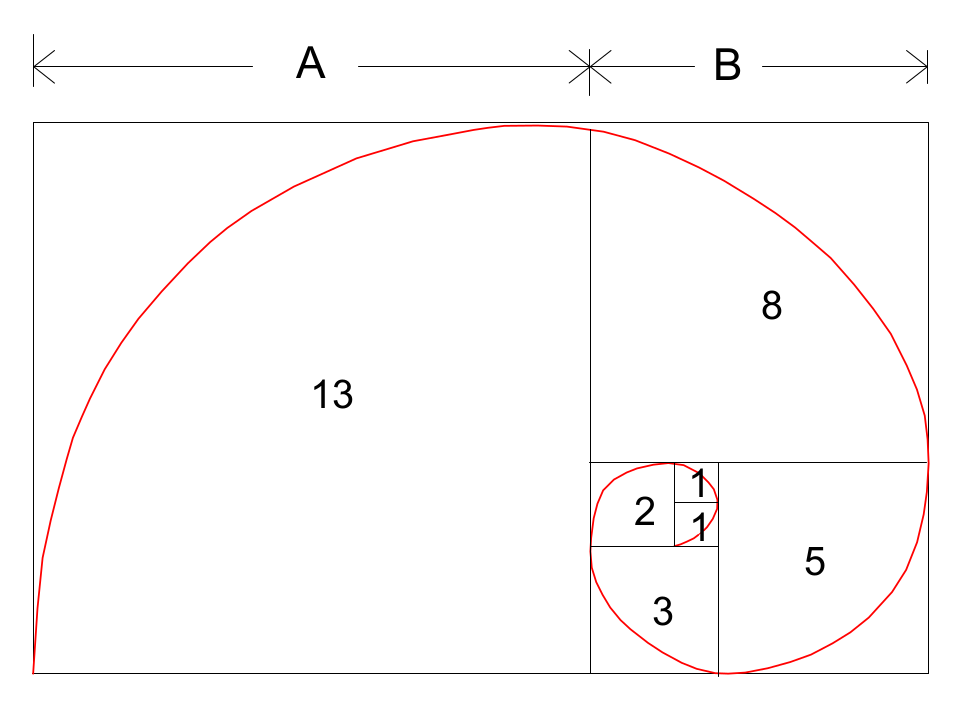(A + B) / A = (13 + 8) / 13 = 1,61538

Im wyższa wartość podstawionych do wzoru wyrazów, tym bardziej zbliżamy się do boskiej proporcji np. (144 + 89) /144 = 1,61805.

Spirala Bernoulliego (logarytmiczna)

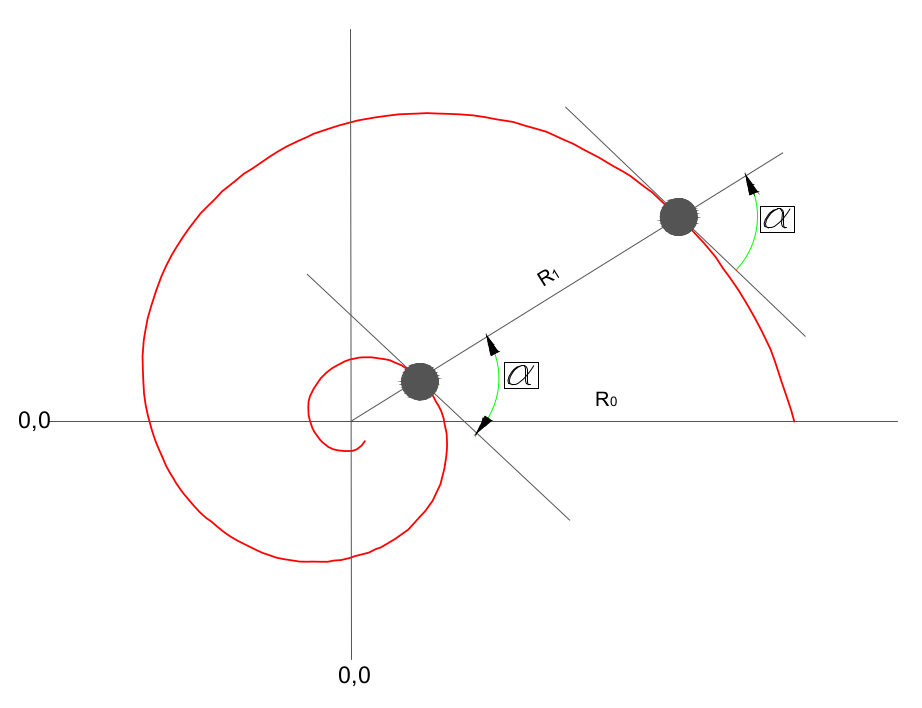
Krzywa płaska przecinająca pod jednakowym, stałym kątem α wszystkie półproste wychodzące z ustalonego punktu, zwanego biegunem spirali. Stąd czasami nazywana jest spiralą równokątną.

Cechy spirali logarytmicznej:

– odległość od środka kolejnych pętel spirali rośnie w postępie geometrycznym,
– wyruszając z dowolnego punktu spirali i idąc po niej można okrążyć biegun dowolną liczbę razy nie dochodząc do niego.

Szczególnym przypadkiem spirali logarytmicznej jest „złota spirala” rysowana w prostokącie o proporcjach boków 1 x 1,618.

Pokrewieństwo spiral Archimedesa, Fibonacciego i Bernouliego

Występuje ścisła korelacja między wymienionymi spiralami. Istotę tego związku z dobrym przybliżeniem ilustruje sprężyna płaska typu napędowego. Sprężyna w stanie zwiniętym jest odzwierciedleniem Spirali Archimedesa, ponieważ odległości między zwojami są identyczne i określone przez grubość metalowej taśmy (Fot. A). Sprężyna w stanie odprężonym zawiera zwoje o zwiększających się wzajemnie odległościach w miarę oddalania się końcówki taśmy od środka (Fot. B).

Fot. A

Fot. B

Rozciągnięcie spirali Archimedesa w przestrzeni trójwymiarowej pozwala na otrzymanie śruby stożkowej typu A, natomiast rozciągnięcia spirali logarytmicznej utworzy śrubę stożkową typu B.

Śruba stożkowa typu A:

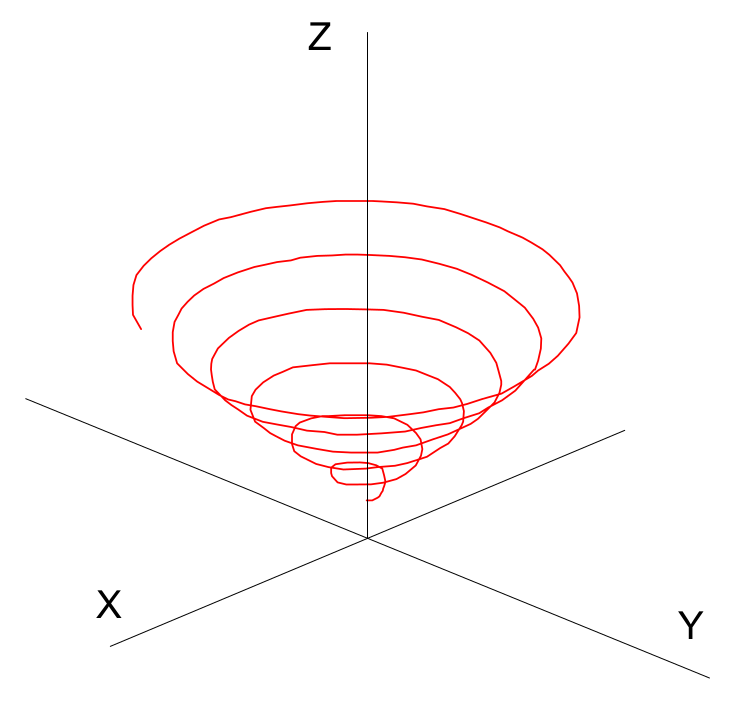
  Śruba stożkowa typu B:

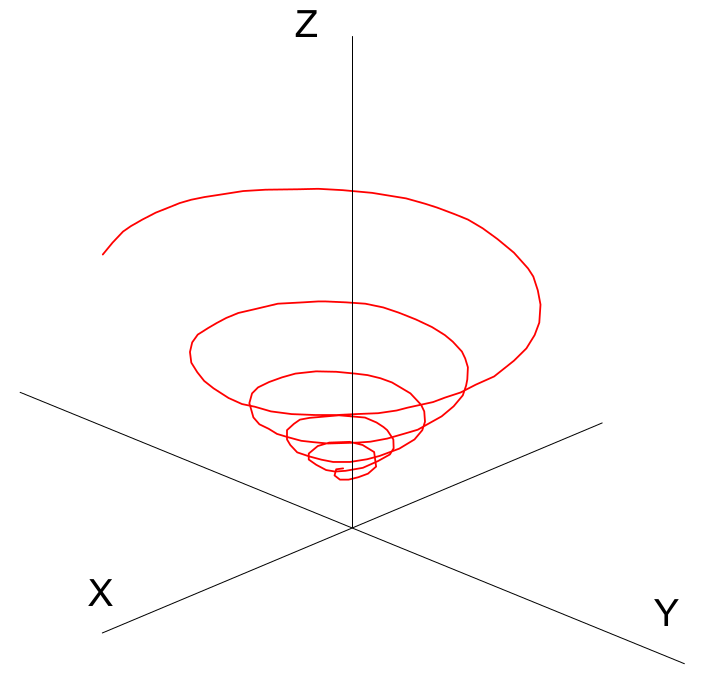
Spirale w środowisku wodnym zaprojektowane przez naturę

Obecność opisanych krzywych, można zaobserwować w wielu zjawiskach i elementach przyrody – w pajęczynie utkanej przez pająka krzyżaka, układzie muszli mięczaków, kwiatostanach roślin, budowie  człowieka i całych galaktyk. Spirale związane z wodą w stanie naturalnym przedstawiają zamieszczone fotografie.

Wir wodny:

Załamanie fali oceanicznej:

Spirale ukryte w urządzeniach wymyślonych przez człowieka.

Wirnik pompy typu vortex: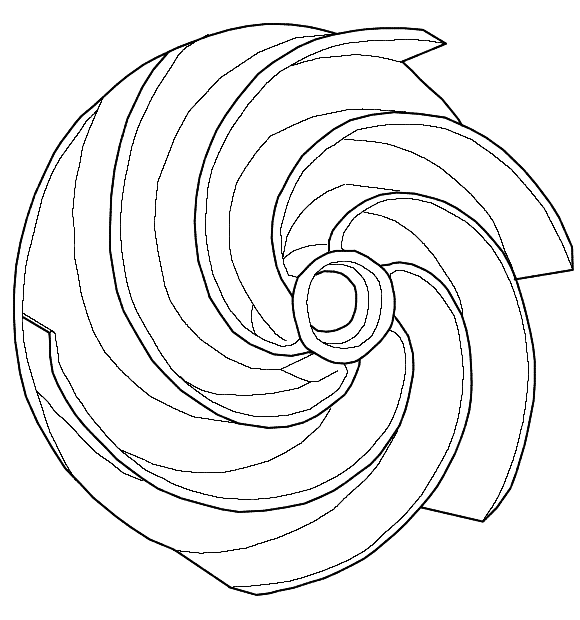

Wirnik pompy typu kanałowego:

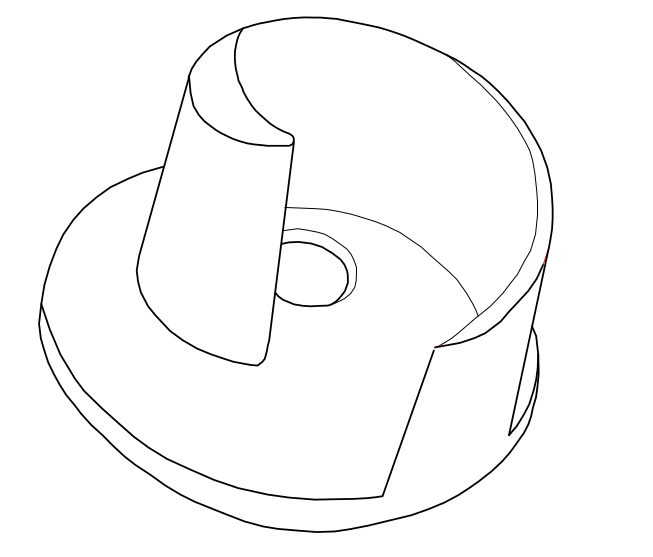
Wirnik pompy typu śrubowo-odśrodkowego:

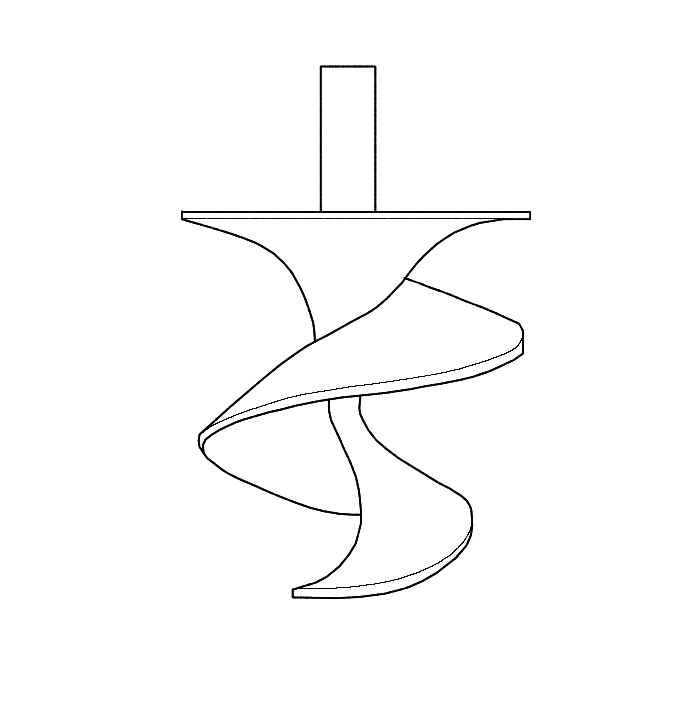
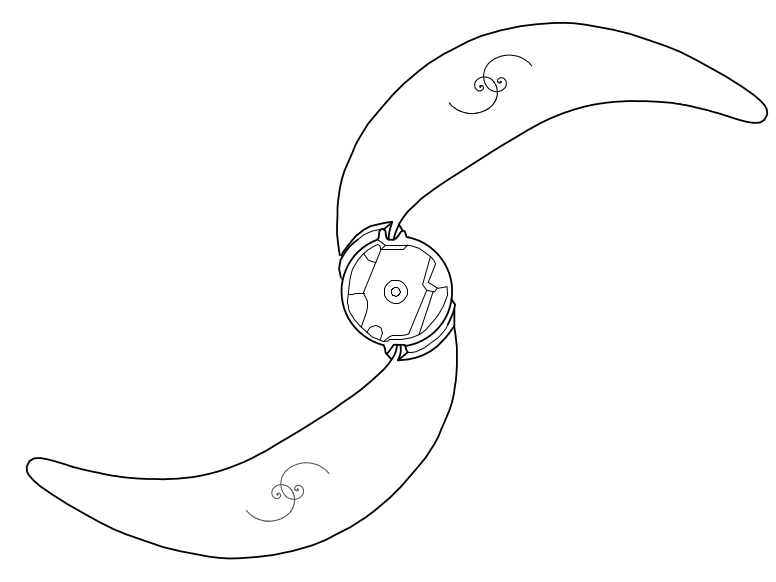
Mieszadło wolnoobrotowe do ścieków:

Zamiast podsumowania

Temat wymienionych w artykule krzywych jest niezmiernie intrygujący, do tego stopnia, że od setek lat rozpalał głowy naukowców. Szczególnie zainteresowanie dotyczyło i nadal dotyczy krzywej Fibonacciego i na pierwszy rzut oka zbliżonej do niej krzywej logarytmicznej z uwagi na dopatrywanie się w nich wymiaru transcendentalnego. W spirali Archimedesa wzrost polega wyłącznie na dodawaniu, natomiast w budowie spirali logarytmicznej uzależniony jest od jej rozmiaru, lepiej oddając prawa przyrody. Dostrzegana obecność omawianych krzywych w wielu tworach natury wydawała się być poznaną cegiełką w budowie wszechświata. Niezliczona ilość prac naukowych i pseudonaukowych dotyczy tajemnicy złotego (boskiego) podziału. Zmysły człowieka błyskawicznie i bezbłędnie, często bez naszej świadomości rozpoznają obecność  w otoczeniu tej proporcji geometrycznej. Jeżeli coś się nam po prostu podoba, po bliższym zbadaniu okazuje się, że jest oparte na złotym podziale. Bezwarunkowo uważamy, że świat przyrody oparty jest na idealnej harmonii, ale harmonię tę znajdujemy również w rezultatach niektórych działań człowieka. Jest to szczególnie widoczne w architekturze i sztukach pięknych,  lecz można regułę złotego podziału odnaleźć również narzędziach i urządzeniach stworzonych przez człowieka, choć jest to już raczej rzadkością. Ja odnalazłem spirale oparte na złotym podziale w pompach i mieszadłach wykorzystywanych w gospodarce wodno – ściekowej, ponieważ z tą dziedziną związany jestem zawodowo.

Zachęcam czytelników by spróbowali sami odnaleźć w swoim otoczeniu, którąś z opisywanych spiral zapisaną w naturze lub wytworze ludzkich rąk.

Jeżeli znajdziecie taką ukrytą spiralę, a nie będzie jej w dostępnych bogatych zasobach internetowych, możecie być z siebie naprawdę dumni. Redakcja bloga „wodkany.pl” chętnie opublikuje wyniki poszukiwań czytelników po podpisaniu stosownego oświadczenia wymaganego prawem zgodnie z ustawą z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych.